Problem 2-4, Determining required sample size

Problem Statement

A normally distributed random variable has an unknown mean $\mu$ and a known variance ${\sigma }^2=9$. Find the sample size required to contruct a 95 percent confidence interval on the mean that has a total length of 1.0.

Solution

Figure 1: Confidence interval of the sample mean.

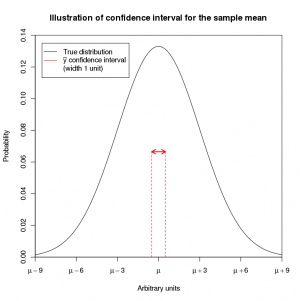
The problem is asking us how much data we need in order to say with 95% certainty that the mean $\mu$ is within a range of length one. We know from previous problems how to calculate the boundaries of a confidence interval for the sample mean, and we are told the total length of the confidence interval should be one. So we begin by subtracting the equation for the left edge of the confidence interval from the equation for the right edge, and setting this equal to one:

$(\mu +\frac{z_{\alpha /2}\sigma }{\sqrt{N}})-(\mu -\frac{z_{\alpha /2}\sigma }{\sqrt{N}})=1$

Simplifying and solving for N, we get:

$N=(2z_{\alpha /2}\sigma {)}^2$

We can plug in for $\sigma$ with the value given in the problem statement, and we can solve for $z_{alpha/2}$ with NORMSINV(1-0.05) in Excel, or qnorm(1-0.05/2) in R (we assumed an $\alpha$ of 0.05).

$N=(2\cdot 1.96\cdot 3{)}^2=138.29$

We can't take a .29th of a datapoint, so we round up to $N=139$.